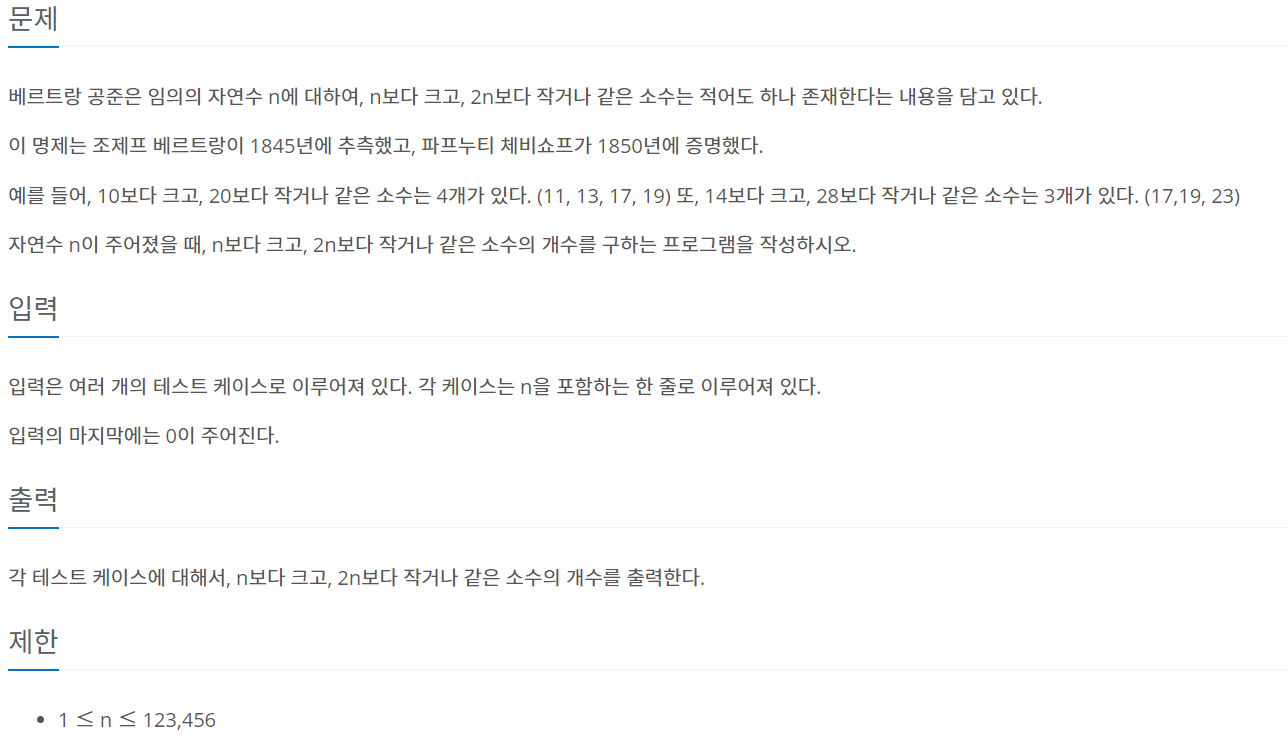
위의 문제를 풀기 위해 에라토스테네스의 체의 원리를 이용했다.
에라토스테네스의 체는 소수를 구하기 위한 알고리즘 중 가장 성능이 좋은 방법으로, 소수의 배수를 거름으로써 건너뛰는 작업이 많아진다.
과정
-
선언
- 2*n 의 최대값이 246912이므로 246913의 소수 여부 배열(boolean)
- 위와 같은 크기의 int배열 선언하여 1부터 소수가 몇 개 있는지 저장
-
값 할당
- 에라토스테네스 체 원리 이용하여 소수 여부를 true로 바꿈
- 2부터 반복문을 이용해 false가 나올 때마다 count를 올려주는 식으로 코드를 구성
-
최종 풀이
- 수를 입력받아 2*n까지의 소수 개수에서 n개까지 소수 개수를 빼고 정답 출력
전체 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
boolean[] check = new boolean[246913];
int[] arr = new int[246913];
check[0] = check[1] = true;
for(int i=2; i<=Math.sqrt(246913);i++) {
if(check[i]==true) continue;
for(int j=i*i; j<=246913; j=j+i) check[j]=true;
}
int count =0;
for(int i=2;i<246913;i++) {
if(!check[i]) count++;
arr[i] = count;
}
int n = 1;
while(true) {
n = sc.nextInt();
if (n==0) break;
System.out.println(arr[2*n] - arr[n]);
}
}
}
|
