시계열 데이터

시계열 데이터 요소

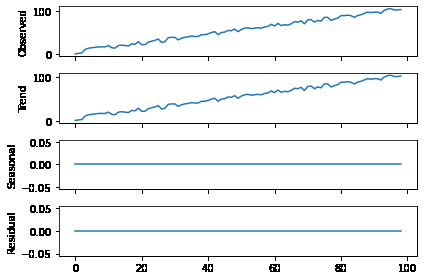
추세(Trend): 장기적으로 나타나는 변동 패턴
계절성(Seasonal): 주,월,분기,반기 단위 등 이미 알려진 시간의 주기로 나타나는 패턴
주기(Cyclic): 고정된 기간이 아닌 장기적인 변동
랜덤요소 (random/residual/remainder)

`비정상 시계열이란 위의 4가지 패턴이 들어가 있는 경우를 말하고 이 요소들을 제거하고 정상화하는 것이 필수적이다.

y_t = Level + Trend + Seasonality + Noise

Stationary(정상성)

평균,분산 공분산이 시간에 따라 변하지 않아야 함.

일반적인 시계열 분석

시각화
시계열 안정
자기상관성 및 parameter 찾기
ARIMA 모델 등으로 예측

안정성을 위한 과정

Differencing

앞 데이터와 뒤 데이터의 차이
stationary하게 만드는 과정 -> d parameter
trend, seasonality가 없어지는 과정 -> 보통 1,2차에서 끝나고 그래도 성능이 좋아지지 않으면 다른 요인의 문제

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


# stationary 확인
from statsmodels.tsa.stattools import adfuller

def adf_check(ts):
    result = adfuller(ts)
    if result[1] <= 0.05:
        print('Stationary {}'.format(result[1]))
    else:
        print('Non-Stationary {}'.format(result[1]))

# 보통 0.05이하가 되어야 
adf_check(timeseries) 

# 1차 차분
diff1 = timeseries - timeseries.shift(1)
adf_check(diff1.dropna())

로그 변환

표준편차가 자료의 크기에 비례하여 증가할 경우

정상과정 확률 모형

가우시안 백색잡음의 현재값과 과거값들의 선형조합으로 이루어져 있다고 가정

Autoregression(AR)

p parameter 관련
데이터와 이전 시점 사이의 관계에 대한 회귀 모델

Moving Average(MA)

q parameter
이전 시점의 moveing average의 residual에 대한 회귀 모델 -> noise 예측

ARMA (Auto-Regressive Moving Average)

AR모형과 MA모형의 특징을 모두 가지는 모형

ARIMA(p,d,q)

Augmented Dickey-Fuller 검정 : d
자기상관계수 함수(ACF): q
편자기상관계수 함수(PACF) : p

acf : 특정 시간만큼 지연된 데이터와 연관성 pacf : t와 t-p의 연관성을 배제하고 보여줌 값이 파란 영역 내에 다 들어가야 p,q를 정할 수 있음 confidence level 보통 95%해서 lag=20으로 두고 2개 이상 올라오지 않으면 correlation이 없다고 생각한다.

모형	ACF	PACF
AR(p)	지수함수적으로 감소하거나 점차 진폭이 축소되는 사인 곡선의 파동을 나타내거나 또는 양쪽모두 나타남 (시차가 증가함에 따라0 으로 급속히 접근)	p 의 시차까지 유의성 있는 값을 나타내고 이후 소멸함
MA(q)	q 의 시차까지 유의성 있는 값을 나타내고 이후 소멸함	지수함수적으로 감소하거나 점차진폭이 축소되는 사인 곡선의 파동을 나타내거나 또는 양쪽 모두 나타남 (시차가 증가함에 따라 0 으로급속히접근)
ARMA(p,q)	지수함수적으로 감소하거나 점차 진폭이 축소되는 사인 곡선의 파동을 나타내거나 또는 양쪽 모두 나타남 (시차가 증가함에 따라 0 으로 급속히 접근)	지수함수적으로 감소하거나 점차 진폭이 축소되는 사인 곡선의 파동을 나타내거나 또는 양쪽 모두 나타남 (시차가 증가함에 따라 0 으로 급속히 접근)

1
2
3
4


from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(diff2.dropna());
plot_pacf(diff2.dropna(),method='ywm');

위 그림에서 대략적으로 acf에서 q=1, p=7로 정해줄 수 있음

SARIMAX

Seasonal ARIMA 모형.

단순 SARIMA 모형은 각 계절에 따른 독립적인 ARIMA 모형이 합쳐져 있는 모형이다. 기존 ARIMA(p,d,q) 모형에 계절성 주기를 나타내는 차수 s가 추가적으로 필요하기 때문에 SARIMA(P,D,Q,s) 로 표기한다. s의 값은 월별 계절성을 나타낼 때는 $s=12$ 가 되고 분기별 계절성을 나타낼 때는 $s=4$ 가 된다

D는 차분 횟수고 P,Q는 위와 같이 ACF, PACF로 구해준다. 아래는 차분을 2번한 것을 s=7로 한 결과이다

1
2
3
4
5
6


diff2_seasonal_diff1 = diff2 - diff2.shift(7)
adf_check(diff2_seasonal_diff1.dropna())
# Stationary 4.042667176872469e-09

plot_acf(diff2_seasonal_diff1.dropna());
plot_pacf(diff2_seasonal_diff1.dropna(),method='ywm');

acf -> Q=2 pacf -> P=3

Modeling

앞의 결과와 합하면 최종적으로 SARIMA (7,2,1)X(3,2,2,7)

1
2
3
4
5
6


import statsmodels.api as sm
model = sm.tsa.statespace.SARIMAX(timeseries,
        order=[7,2,1],seasonal_order=[3,2,2,7])

result = model.fit()
result.summary()

result.plot_diagnostics()를 통해 정규성, 정상성 여부 등 확인

forecast

1
2
3
4


pred = result.predict(start='2020-08-14',end='2020-09-13', )
train['Confirmed'].plot(label='Train')
test['Confirmed'].plot(label='Test')
pred.plot(label='pred')

Rolling forecast

일정 구간을 train, 다음 것을 예측을 반복

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


from statsmodels.tsa.arima_model import ARIMA
import itertools

# 파라미터 조합 만들기
p = list(range(0,6))
d= [1,2]
q = list(range(0,2))
pdq = list(itertools.product(p,d,q))

for params in pdq:
    model = ARIMA(timeseries, order=params)
    result = model.fit(disp=-1)
    print('ARIMA{}  AIC : {}'.format(params,result.aic))

ARIMA(0, 1, 0)  AIC : 3935.7017097744483
ARIMA(0, 1, 1)  AIC : 3937.582587394849
ARIMA(0, 2, 0)  AIC : 4061.9453403812095
ARIMA(0, 2, 1)  AIC : 3924.744203746418
ARIMA(1, 1, 0)  AIC : 3937.590721228459
....

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


predictions = []
history = [x for x in timeseries]
for t in range(len(test)):
    model = ARIMA(history, order=(4,1,3))
    result = model.fit(disp=0)
    output = result.forecast()
    yhat = output[0]
    predictions.append(yhat)
    obs = test['Confirmed'][t]
    history.append(obs)


plt.plot(np.asarray(test['Confirmed']))
plt.plot(predictions)

참고 : 작년 코로나 데이터 분석한 것을 복습 + 추가 개념 정리 Corona data anaylsis 자주 쓰는 numpy/pandas (https://h3imdallr.github.io/2017-08-19/arima/)

시계열 데이터 이해